Volume Of A Sphere Integral Proof

Also recall the chapter prelude, which showed the opera house l'Hemisphèric in Valencia, Spain. It has four sections with one of the sections being a theater in a five-story-high sphere under an oval roof as long as a football field. Inside is an IMAX screen that changes the sphere into a planetarium with a sky full of \(9000\) twinkling stars. Using triple integrals in spherical coordinates, we can find the volumes of different geometric shapes like these.

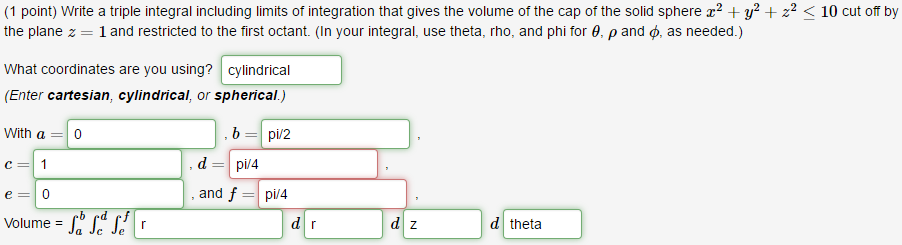
Let D be a smaller cap cut from a solid ball of radius 8 units by a plane 7 units from the center of the sphere. Set up the triple integral for the volume of D in spherical coordinates. Now that we can parameterize surfaces and we can calculate their surface areas, we are able to define surface integrals.

First, let's look at the surface integral of a scalar-valued function. Informally, the surface integral of a scalar-valued function is an analog of a scalar line integral in one higher dimension. Therefore, the definition of a surface integral follows the definition of a line integral quite closely. For scalar line integrals, we chopped the domain curve into tiny pieces, chose a point in each piece, computed the function at that point, and took a limit of the corresponding Riemann sum. For scalar surface integrals, we chop the domain region into tiny pieces and proceed in the same fashion. As stated before, spherical coordinate systems work well for solids that are symmetric around a point, such as spheres and cones.

Let us look at some examples before we consider triple integrals in spherical coordinates on general spherical regions. Using this method, Archimedes was able to show that a cone had the same volume as a a pyramid with the same base area and height. Relates a triple integral of derivative divF over a solid to a flux integral of F over the boundary of the solid. More specifically, the divergence theorem relates a flux integral of vector field F over a closed surface S to a triple integral of the divergence of F over the solid enclosed by S.

The definition is analogous to the definition of the flux of a vector field along a plane curve. Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in Table \(\PageIndex\). These equations will become handy as we proceed with solving problems using triple integrals.

A similar situation occurs with triple integrals, but here we need to distinguish between cylindrical symmetry and spherical symmetry. In this section we convert triple integrals in rectangular coordinates into a triple integral in either cylindrical or spherical coordinates. For now, we are only interested in solids, whose volumes are generated through cross-sections that are easy to describe. For solids of revolution, the volume slices are often disks and the cross-sections are circles. The method of disks involves applying the method of slicing in the particular case in which the cross-sections are circles, and using the formula for the area of a circle. Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones.

Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions. In our daily life, we come across different types of spheres. Basketball, football, table tennis, etc. are some of the common sports that are played by people all over the world. The balls used in these sports are nothing but spheres of different radii. The volume of sphere formula is useful in designing and calculating the capacity or volume of such spherical objects. You can easily find out the volume of a sphere if you know its radius.

We can use triple integrals and spherical coordinates to solve for the volume of a solid sphere. The divergence theorem translates between the flux integral of closed surface S and a triple integral over the solid enclosed by S. In this section, we state the divergence theorem, which is the final theorem of this type that we will study. We use the theorem to calculate flux integrals and apply it to electrostatic fields. In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections.

So far, our examples have all concerned regions revolved around the x\text[/latex] but we can generate a solid of revolution by revolving a plane region around any horizontal or vertical line. On the other hand, when we defined vector line integrals, the curve of integration needed an orientation. That is, we needed the notion of an oriented curve to define a vector line integral without ambiguity. Similarly, when we define a surface integral of a vector field, we need the notion of an oriented surface. An oriented surface is given an "upward" or "downward" orientation or, in the case of surfaces such as a sphere or cylinder, an "outward" or "inward" orientation. The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes.

Note that \(dV\) and \(dA\) mean the increments in volume and area, respectively. The variables \(V\) and \(A\) are used as the variables for integration to express the integrals. Use spherical coordinates to find the volume of the triple integral, where ??? Before calculating this flux integral, let's discuss what the value of the integral should be.

The field is rotational in nature and, for a given circle parallel to the xy-plane that has a center on the z-axis, the vectors along that circle are all the same magnitude. That is how we can see that the flow rate is the same entering and exiting the cube. The flow into the cube cancels with the flow out of the cube, and therefore the flow rate of the fluid across the cube should be zero. The divergence theorem relates a flux integral across a closed surface S to a triple integral over solid E enclosed by the surface. ¶We have seen how to compute certain areas by using integration; we will now look into how some volumes may also be computed by evaluating an integral. Generally, the volumes that we can compute this way have cross-sections that are easy to describe.

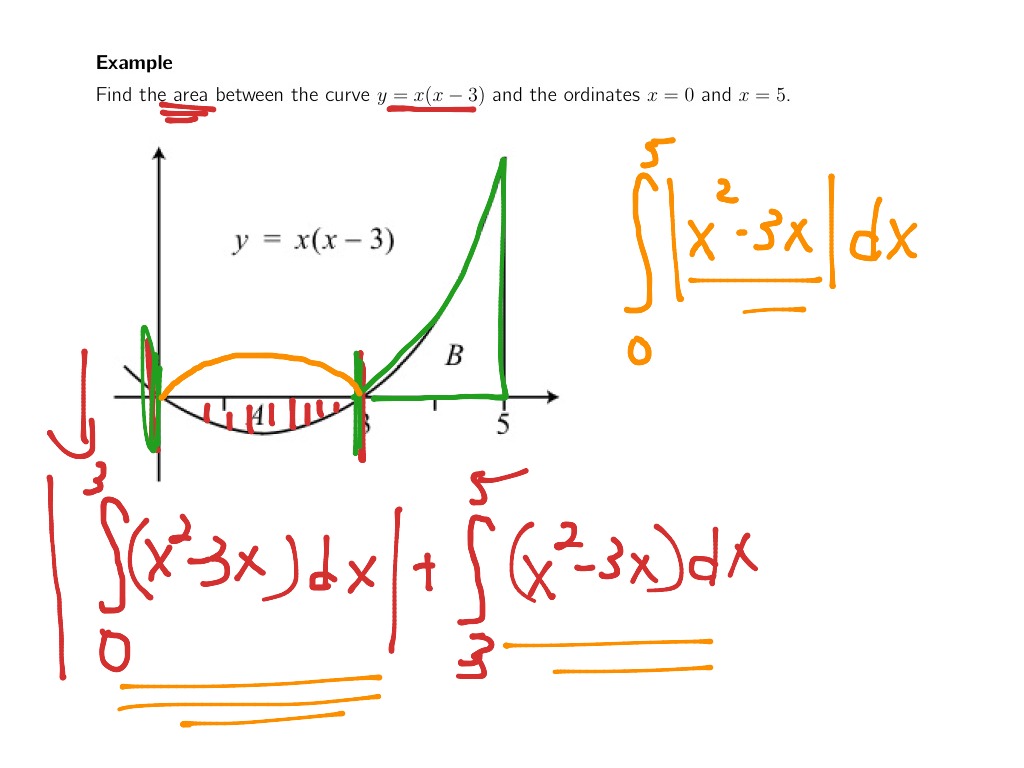
For example, circular cross-sections are easy to describe as their area just depends on the radius, and so they are one of the central topics in this section. However, we first discuss the general idea of calculating the volume of a solid by slicing up the solid. In order to find limits of integration for the triple integral, we'll say that ???

Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids.

When either of the above area is rotated about its axis of rotation, then the solid of revolution that is created has a hole on the inside — like a distorted donut. If we now slice the solid perpendicular to the axis of rotation, then the cross-section shows a disk with a hole in it as indicated below. Such a disk looks like a "washer" and so the method that employs these disks for finding the volume of the solid of revolution is referred to as the Washer Method. The following example demonstrates how to find a volume that is created in this fashion.

Let us now turn towards the calculation of such volumes by working through two examples. The right pyramid with square base shown in Figure 3.11 has cross-sections that must be squares if we cut the pyramid parallel to its base. The following example makes use of these cross-sections to calculate the volume of the pyramid for a certain height. One for the cone underneath of plane and one for the sphere underneath the plane. One of the most remarkable and important mathematical results obtained by Archimedes was the determination of the volume of a sphere. Archimedes used a technique of sub-dividing the volume into slices of known cross-sectional area and adding up, or integrating, the volumes of the slices.

This was essentially an application of a technique that was — close to two thousand years later — formulated as integral calculus. Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. Sometimes, this is just a result of the way the region of revolution is shaped with respect to the axis of revolution. In other cases, cavities arise when the region of revolution is defined as the region between the graphs of two functions. A third way this can happen is when an axis of revolution other than the x\text[/latex] or y\text[/latex] is selected. Since some surfaces are nonorientable, it is not possible to define a vector surface integral on all piecewise smooth surfaces.

This is in contrast to vector line integrals, which can be defined on any piecewise smooth curve. We have seen that a line integral is an integral over a path in a plane or in space. We can extend the concept of a line integral to a surface integral to allow us to perform this integration. The intersection of a plane that contains the normal with the surface will form a curve that is called a normal section, and the curvature of this curve is the normal curvature. For most points on most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures.

Any closed surface will have at least four points called umbilical points. At an umbilic all the sectional curvatures are equal; in particular the principal curvatures are equal. The sphere and plane are the only surfaces with this property. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry.

Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere.

There are two types of spheres, solid sphere, and hollow sphere. We will learn in the following sections about their volumes. About 1800 years prior to the discovery of calculus, Archimedes showed that the surface area of a sphere of radius is .

He also showed that the volume of a ball of radius is using the Cavalieri's principle, again without calculus . Archimedes invented a method that was later re-discovered and became known as Cavalieri's principle. This involves slicing solids with a family of parallel planes.

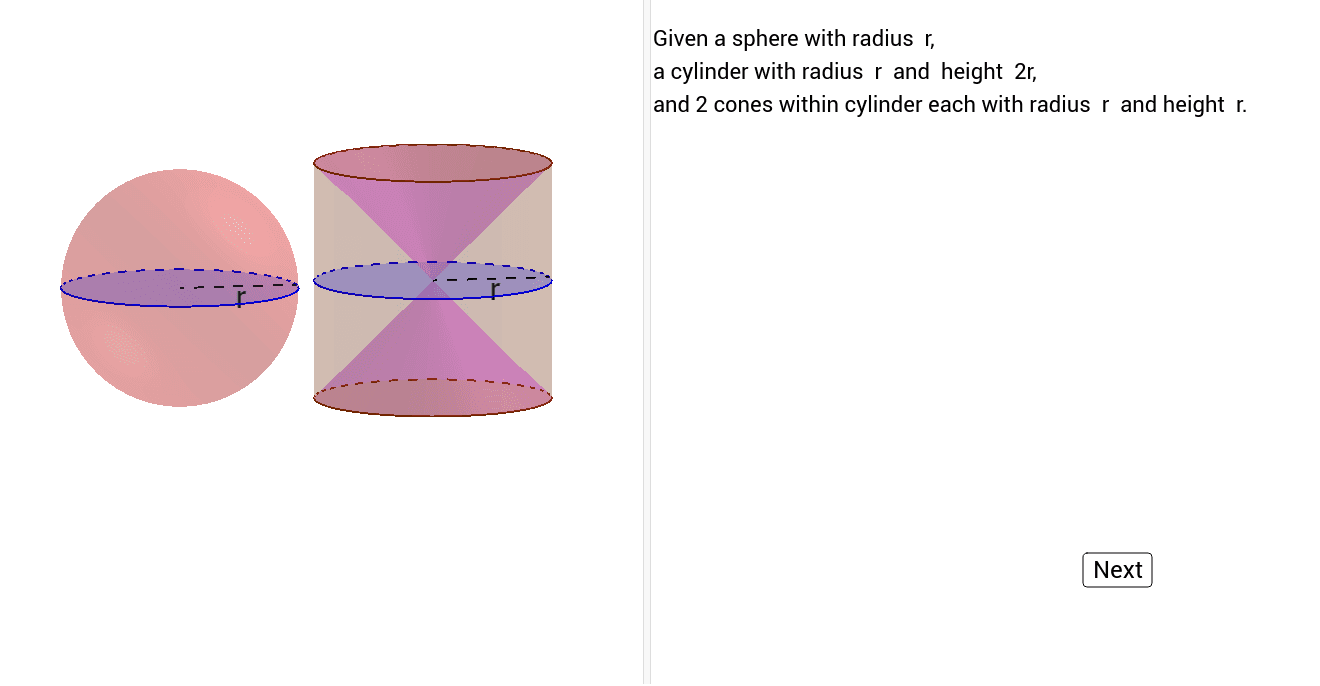
In particular, if we have two solids and if each plane cuts them both into cross-sections of equal area, then the two solids have equal volumes. It is far from obvious from the figure above how the cone and sphere add up to the cylinder. However, if we `rearrange' the conic volume, things become clearer. We note that a cone with half the height () has half the volume. So, we replace the cone by a double cone, each half of height , with centre-point at the centre of the sphere . Now it is clear that in a horizontal slice, the cross-section of the sphere is greatest at the equator and least at the poles.

Contrariwise, the cross-section of the cone is greatest near the top and bottom, and least near the centre-point. Thus, it is not unreasonable to speculate that the sum of the two cross-section areas might be equal. If a solid of revolution has a cavity in the center, the volume slices are washers.

With the method of washers, the area of the inner circle is subtracted from the area of the outer circle before integrating. Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. Also on that page you will see an explanation of the 4/3 in the volume of the sphere.

In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere. The volume of a pyramid is 1/3 times the area of the base times the height. Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle.

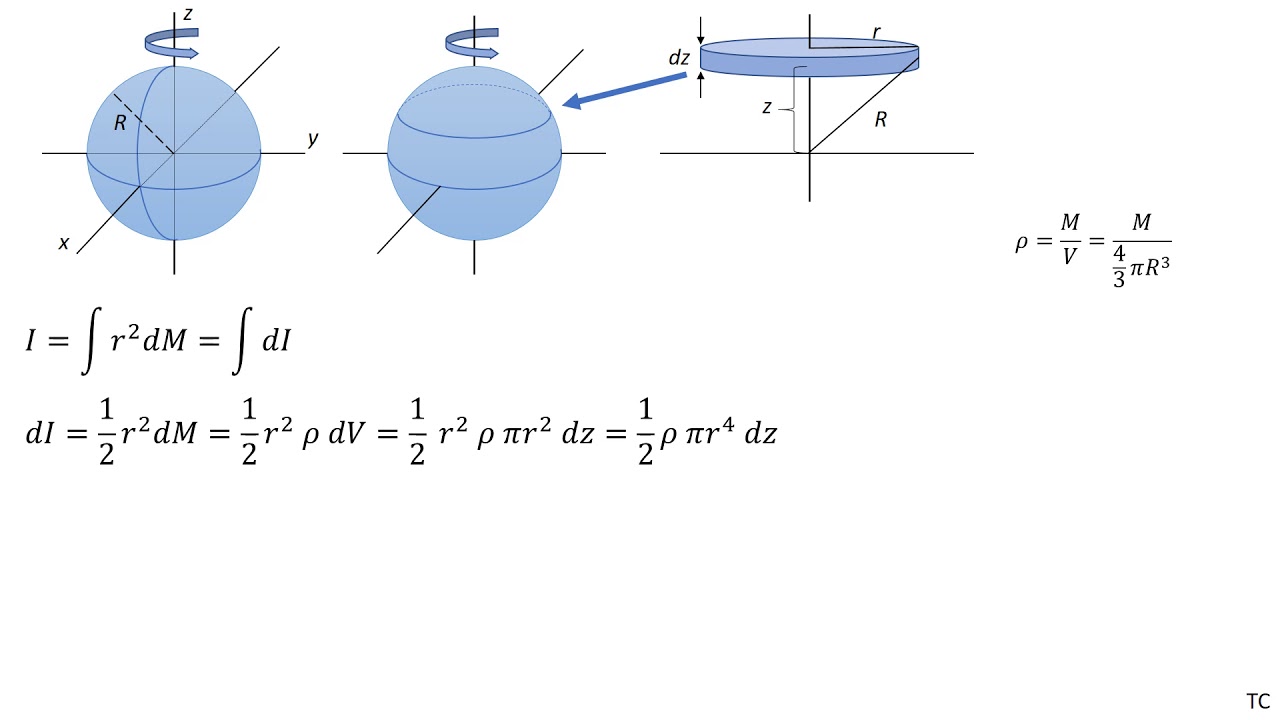
The sphere is there for comparison; the cylinder has had a cone drilled out from the top and the bottom, leaving solid material around it. We're going to slice both the cylinder and the sphere at a height h above the center. Consider a sphere of radius r and divide it into pyramids.

In this way, we see that the volume of the sphere is the same as the volume of all the pyramids of height, r and total base area equal to the surface area of the sphere as shown in the figure. How to perform a triple integral when your function and bounds are expressed in spherical coordinates. In the following problems, students will calculate the volume of a sphere using the formula derived in the lesson. Then, students will derive the formula for the volume of a hemisphere using a similar integration technique. Last, students will use their new formula to find the volume of a specific hemisphere. The following picture is the cross section of the inscribed sphere along the plane, which then becomes a circle of radius inscribed in a square of side .

Volume Of A Sphere Derivation Integral There are so many examples of spherical objects in our day-to-day life. Just remember or derive the formula and calculate the volume for applications. Calculating the flux integral directly would be difficult, if not impossible, using techniques we studied previously. At the very least, we would have to break the flux integral into six integrals, one for each face of the cube. But, because the divergence of this field is zero, the divergence theorem immediately shows that the flux integral is zero.

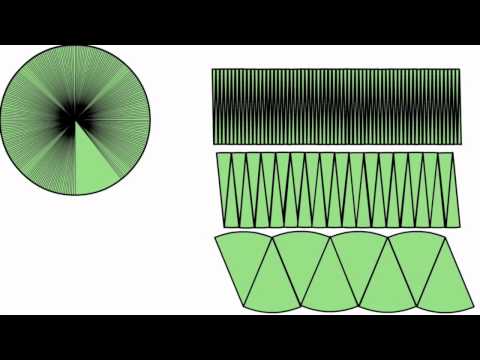
States that given two solids of the same height, whose cross-sections, taken at the same distance above the base, are of equal area, then the solids have the same volume. In this blog, I used polar coordinates to derive the well-known expression for the area of a circle, . In today's blog, I will go from 2 to 3-dimensions to derive the expression for the surface area of a sphere, which is . To do this, we need to use the 3-dimensional equivalent of polar coordinates, which are called spherical polar coordinates.

He rose to the challenge masterfully, becoming the first person to calculate and prove the formulas for the volume and the surface area of a sphere. The method he used is called the method of exhaustion, developed rigorously about a century earlier by one of Archimedes' heroes, Eudoxus of Cnidus. Ok, now let's get a sphere of radius R and slice it in half to make a hemisphere. Next we'll get a cylinder of radius R and height R, and we'll scoop a cone out of it to make a sort of bowl . The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. For the following exercises, draw the region bounded by the curves.