Find The Exact Circumference Of A Circle With The Given Radius

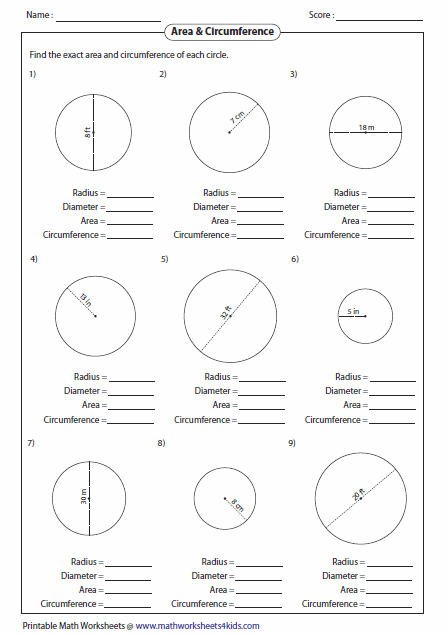
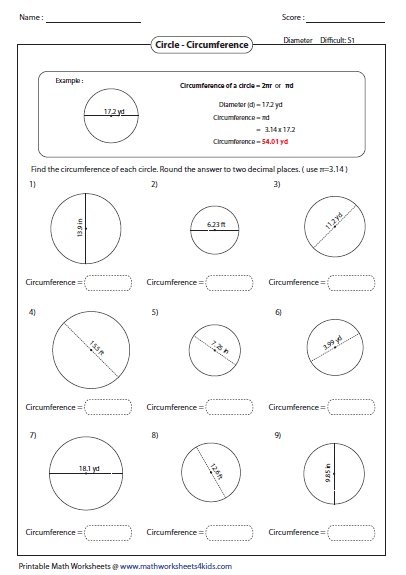
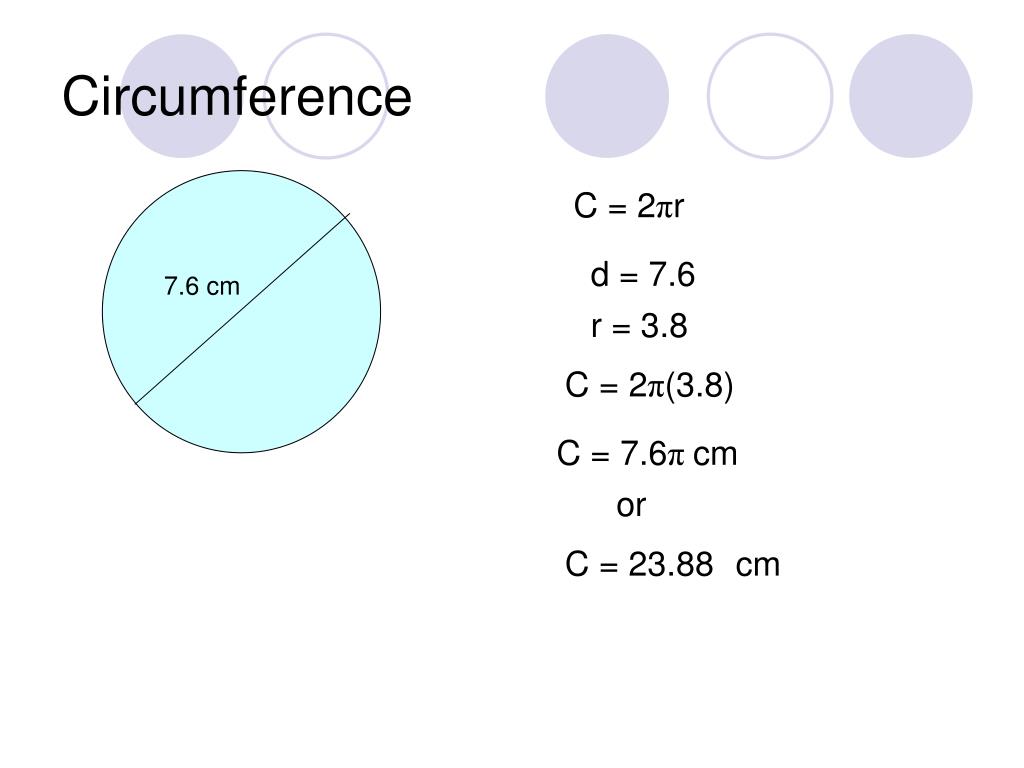
This calculator is quite easy to use and provides you the precise measurements within a couple of seconds. The circumference of a circle calculator not only calculate circumference accurately, but also the other parameters that mentioned above. The circumference of a circle of radius $r$ is $2\pi r$.

This well known formula is taken up here from the point of view of similarity. It is important to note in this task that the definition of $\pi$ already involves the circumference of a circle, a particular circle. In order to show that the ratio of circumference to diameter does not depend on the size of the circle, a similarity argument is required. Two different approaches are provided, one using the fact that all circles are similar and a second using similar triangles.

This former approach is simpler but the latter has the advantage of leading into an argument for calculating the area of a circle. The circumference of a circle is the measurement around a circle's edge. It can be compared to finding the perimeter of a shape . If you were to cut a circle and lay the outline flat, the length of the line it created would be its circumference. The circumference can be measured in any unit or system that traditionally measures length - imperial (inches, feet, etc.) or metric (centimeters, meters, etc.).

Whichever unit the radius is measured in will also be the unit the circumference is calculated in. This first argument is an example of MP7, Look For and Make Use of Structure. The key to this argument is identifying that all circles are similar and then applying the meaning of similarity to the circumference. The second argument exemplifies MP8, Look For and Express Regularity in Repeated Reasoning. Here the key is to compare the circle to a more familiar shape, the triangle. So here the circumference is just equal to, well pi times 23.1, That's approximately 3.14 times 23.1, which is approximately 73.

So there's a conference here is approximately 73 mm. Calculating areas and circumferences of circles plays an important role in almost all field of science and real life. For instance, formula for circumference and area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations. An arch length is a portion of the circumference of a circle.

The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to $360$ degrees. A sector of a circles is the region bounded by two radii of the circle and their intercepted arc. For any other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the area and lengths of parts of a circle. The first solution requires a general understanding of similarity of shapes while the second requires knowledge of similarity specific to triangles.

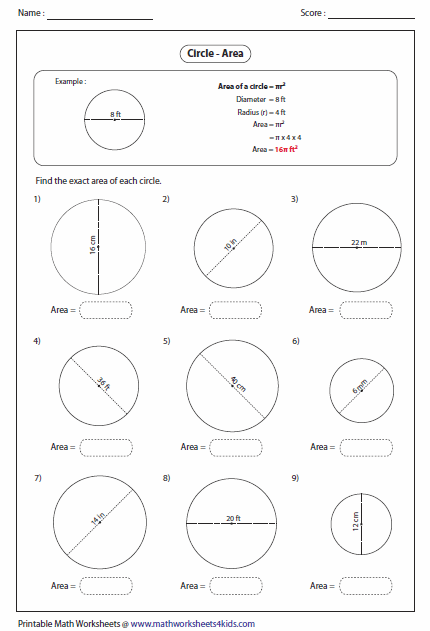
To find the area of a circle with the radius, square the radius, or multiply it by itself. Then, multiply the squared radius by pi, or 3.14, to get the area. To find the area with the diameter, simply divide the diameter by 2, plug it into the radius formula, and solve as before. This give a geometric justification that the area of a circle really is "pi r squared". We'll teach you the key circumference formulas you need to figure out the circumference of a circle when you know either the diameter or radius. The diameter of a circle is twice to that of the radius.

If the diameter or radius of a circle is given, then we can easily find the circumference. We can also find the diameter and radius of a circle if the circumference is given. We round off to 3.14 in order to simplify our calculations. Circumference, diameter and radii are calculated in linear units, such as inches and centimeters. A circle has many different radii and many different diameters, and each one passes through the center. This concept can be of significance in geometry, to find the perimeter, area and volume of solids.

Real life problems on circles involving arc length, sector of a circle, area and circumference are very common, so this concept can be of great importance of solving problems. The radius, the diameter, and the circumference are the three defining aspects of every circle. Given the radius or diameter and pi you can calculate the circumference.

The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle. You can also think of the radius as the distance between the center of the circle and its edge. To understand how to calculate circumference we must first begin with the definition of circumference. Circumference of a circle is linear distance around outer border of a circle.

To find out the circumference, we need to know its diameter which is the length of its widest part. The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . Area and circumference of circle calculator uses radius length of a circle, and calculates the perimeter and area of the circle. It is an online Geometry tool requires radius length of a circle. Using this calculator, we will understand methods of how to find the perimeter and area of a circle. The distance around a polygon, such as a square or a rectangle, is called the perimeter .

On the other hand, the distance around a circle is referred to as the circumference . Therefore, the circumference of a circle is the linear distance of an edge of the circle. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye. While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters.

What is the approximate circumference of the ferris wheel? Apart from these formulas, you simply add the value into the designated filed of the diameter of a circle calculator to find the diameter of the circle instantly. Not just this but there are some significant distances on a circle that needs to be calculated before finding the circumference of the circle. Diameter is the distance from one side of the circle to the other, crossing through the center/ middle of the circle.

Does calculating circumference have you running in circles? Our circumference calculator is an easy way for you to find the circumference of any circular object. The distance from the centre to the outer line of the circle is called a radius. It is the most important quantity of the circle based on which formulas for the area and circumference of the circle are derived. Twice the radius of a circle is called the diameter of the circle.

The diameter cuts the circle into two equal parts, which is called a semi-circle. When we use the formula to calculate the circumference of the circle, then the radius of the circle is taken into account. Hence, we need to know the value of the radius or the diameter to evaluate the perimeter of the circle. To calculate the diameter of a circle, multiply the radius by 2. If you don't have the radius, divide the circumference of the circle by π to get the diameter. If you don't have the radius or the circumference, divide the area of the circle by π and then find that number's square root to get the radius.

The circumference of a circle is equal to pi times the diameter. Radius is the measured distance from the centre of a circle to the edge. If you don't know the radius but you do know the total width of the circle finding the radius is a snap. The circle's width is known as diameter.

If you know the circumference, radius, or diameter of a circle, you can also find its area. Area represents the space enclosed within a circle. It's given in units of distance squared, such as cm2 or m2. The Greek letter p (pronounced as "pie") is used to describe this number. It stands for the ratio between the circumference of any circle and its diameter, and it's true for all circles. This means that any circle's circumference will be about 3.14 times the length of its diameter.

Π shows the ratio of the perimeter of a circle to the diameter. Therefore, when you divide the circumference by the diameter for any circle, you obtain a value close enough to π. This relationship can be explained by the formula mentioned below. As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape. The circumference of a circle is the same as the length of a straight line folded or bent to make the circle.

The circumference of a circle is measured in meters, kilometers, yards, inches, etc. Use this circle calculator to find the area, circumference, radius or diameter of a circle. Given any one variable A, C, r or d of a circle you can calculate the other three unknowns.

The distance around a rectangle or a square is as you might remember called the perimeter. The distance around a circle on the other hand is called the circumference . The circumference of a circle is \(\pi\) times its diameter or \(2 \pi\) times its radius, where \(\pi\) is approximately 3.14. The properties of circles have been studied for over 2,000[/latex] years.

All circles have exactly the same shape, but their sizes are affected by the length of the radius, a line segment from the center to any point on the circle. A line segment that passes through a circle's center connecting two points on the circle is called a diameter. The diameter is twice as long as the radius. In its simplest form, the ratio of a circle circumference to its radius is 2 Pi (π) to 1. For every single unit of radius, there are 2 is 2 Pi (π) units in the circumference.

The surface area of a sphere is refers to exactly four times the area of a circle with the same radius. For a better understanding, you can look at the given formula of surface area of a sphere. A radius of circle is referred to as a straight line from the center of a circle to the circumference of a circle.

And, if you have two or more of them, they're said to be as radii. The plural for is radii that is pronounced as "ray-dee-eye" and remember that all radii in a circle will be the same length. The circumference is an important property of circle; it is referring as the distance around the outside of the circle. In simple words, it is the linear distance of a circle's edge.

Find The Area Of A Circle With Circumference 32 U03c0 The circumference is similar to the perimeter of a geometric figure but remembers that 'perimeter' is the term that is only used for polygons. In this worksheet, we will practice finding the circumference of a circle using the formula 2πr and solving problems involving quarter circles and semicircles. The circumference of a circle is merely the distance around a circle. Sometimes it is referred to as the perimeter, although the term perimeter is usually reserved for the measure of a distance around a polygon. Thus, we can define three different formulas to find the perimeter of circle (i.e. circumference of a circle).

Pi (π) is a special mathematical constant; it is the ratio of circumference to diameter of any circle. A circle is 360° all the way around; therefore, if you divide an arc's degree measure by 360°, you find the fraction of the circle's circumference that the arc makes up. Then, if you multiply the length all the way around the circle (the circle's circumference) by that fraction, you get the length along the arc. There are two ways of finding the perimeter or circumference of a circle. The first formula involves using the radius, and the second involves using the diameter of a circle. It is important to note that both two methods yield the same result.

You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference. Understanding what a circumference of a circle is and how to calculate it is crucial as you move to higher level math. In this article you will learn the answers to the following questions. If your radius is a mixed number, turn the number into an improper fraction.

To do this, simply multiply the whole number part by the denominator and add that number to the numerator. The denominator should remain the same throughout the process. You can then use the improper fraction in your formula.

The circumference of a circle is refers three times to its diameter approximately. The distance around the edge of the circle is said to be as the circumference of a circle. While, the distance from one side of the circle to other, which going through the center of the circle is referred to as the diameter.

Also, our circumference of a circle calculator follows the same way for finding the circumference of a circle. The area of a circle calculator by calculator-online is also uses the same formula to find the area of a circle. The diameters of a circle the measurement referred to as the length of the line through the center and touching two points on its edge. The diameter is something that measures how big the circle is from rim to rim passing through the center.

The following function uses Math.PI to calculate the circumference of a circle with a passed radius. This proportion of circumference to diameter is the description of the constant pi. It is used in different areas, such as physics and mathematics. Circumference of a circle is the linear distance that is measured along its sides. It is parallel to perimeter of a geometric figure, but the term 'perimeter' is rather used to describe the property of polygons. Circumference is often wrongly spelled as circumfrence.

Volume Of A Sphere Integral Proof

Also recall the chapter prelude, which showed the opera house l'Hemisphèric in Valencia, Spain. It has four sections with one of the sections being a theater in a five-story-high sphere under an oval roof as long as a football field. Inside is an IMAX screen that changes the sphere into a planetarium with a sky full of \(9000\) twinkling stars. Using triple integrals in spherical coordinates, we can find the volumes of different geometric shapes like these.

Let D be a smaller cap cut from a solid ball of radius 8 units by a plane 7 units from the center of the sphere. Set up the triple integral for the volume of D in spherical coordinates. Now that we can parameterize surfaces and we can calculate their surface areas, we are able to define surface integrals.

First, let's look at the surface integral of a scalar-valued function. Informally, the surface integral of a scalar-valued function is an analog of a scalar line integral in one higher dimension. Therefore, the definition of a surface integral follows the definition of a line integral quite closely. For scalar line integrals, we chopped the domain curve into tiny pieces, chose a point in each piece, computed the function at that point, and took a limit of the corresponding Riemann sum. For scalar surface integrals, we chop the domain region into tiny pieces and proceed in the same fashion. As stated before, spherical coordinate systems work well for solids that are symmetric around a point, such as spheres and cones.

Let us look at some examples before we consider triple integrals in spherical coordinates on general spherical regions. Using this method, Archimedes was able to show that a cone had the same volume as a a pyramid with the same base area and height. Relates a triple integral of derivative divF over a solid to a flux integral of F over the boundary of the solid. More specifically, the divergence theorem relates a flux integral of vector field F over a closed surface S to a triple integral of the divergence of F over the solid enclosed by S.

The definition is analogous to the definition of the flux of a vector field along a plane curve. Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in Table \(\PageIndex\). These equations will become handy as we proceed with solving problems using triple integrals.

A similar situation occurs with triple integrals, but here we need to distinguish between cylindrical symmetry and spherical symmetry. In this section we convert triple integrals in rectangular coordinates into a triple integral in either cylindrical or spherical coordinates. For now, we are only interested in solids, whose volumes are generated through cross-sections that are easy to describe. For solids of revolution, the volume slices are often disks and the cross-sections are circles. The method of disks involves applying the method of slicing in the particular case in which the cross-sections are circles, and using the formula for the area of a circle. Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones.

Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions. In our daily life, we come across different types of spheres. Basketball, football, table tennis, etc. are some of the common sports that are played by people all over the world. The balls used in these sports are nothing but spheres of different radii. The volume of sphere formula is useful in designing and calculating the capacity or volume of such spherical objects. You can easily find out the volume of a sphere if you know its radius.

We can use triple integrals and spherical coordinates to solve for the volume of a solid sphere. The divergence theorem translates between the flux integral of closed surface S and a triple integral over the solid enclosed by S. In this section, we state the divergence theorem, which is the final theorem of this type that we will study. We use the theorem to calculate flux integrals and apply it to electrostatic fields. In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections.

So far, our examples have all concerned regions revolved around the x\text[/latex] but we can generate a solid of revolution by revolving a plane region around any horizontal or vertical line. On the other hand, when we defined vector line integrals, the curve of integration needed an orientation. That is, we needed the notion of an oriented curve to define a vector line integral without ambiguity. Similarly, when we define a surface integral of a vector field, we need the notion of an oriented surface. An oriented surface is given an "upward" or "downward" orientation or, in the case of surfaces such as a sphere or cylinder, an "outward" or "inward" orientation. The concept of triple integration in spherical coordinates can be extended to integration over a general solid, using the projections onto the coordinate planes.

Note that \(dV\) and \(dA\) mean the increments in volume and area, respectively. The variables \(V\) and \(A\) are used as the variables for integration to express the integrals. Use spherical coordinates to find the volume of the triple integral, where ??? Before calculating this flux integral, let's discuss what the value of the integral should be.

The field is rotational in nature and, for a given circle parallel to the xy-plane that has a center on the z-axis, the vectors along that circle are all the same magnitude. That is how we can see that the flow rate is the same entering and exiting the cube. The flow into the cube cancels with the flow out of the cube, and therefore the flow rate of the fluid across the cube should be zero. The divergence theorem relates a flux integral across a closed surface S to a triple integral over solid E enclosed by the surface. ¶We have seen how to compute certain areas by using integration; we will now look into how some volumes may also be computed by evaluating an integral. Generally, the volumes that we can compute this way have cross-sections that are easy to describe.

For example, circular cross-sections are easy to describe as their area just depends on the radius, and so they are one of the central topics in this section. However, we first discuss the general idea of calculating the volume of a solid by slicing up the solid. In order to find limits of integration for the triple integral, we'll say that ???

Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids.

When either of the above area is rotated about its axis of rotation, then the solid of revolution that is created has a hole on the inside — like a distorted donut. If we now slice the solid perpendicular to the axis of rotation, then the cross-section shows a disk with a hole in it as indicated below. Such a disk looks like a "washer" and so the method that employs these disks for finding the volume of the solid of revolution is referred to as the Washer Method. The following example demonstrates how to find a volume that is created in this fashion.

Let us now turn towards the calculation of such volumes by working through two examples. The right pyramid with square base shown in Figure 3.11 has cross-sections that must be squares if we cut the pyramid parallel to its base. The following example makes use of these cross-sections to calculate the volume of the pyramid for a certain height. One for the cone underneath of plane and one for the sphere underneath the plane. One of the most remarkable and important mathematical results obtained by Archimedes was the determination of the volume of a sphere. Archimedes used a technique of sub-dividing the volume into slices of known cross-sectional area and adding up, or integrating, the volumes of the slices.

This was essentially an application of a technique that was — close to two thousand years later — formulated as integral calculus. Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. Sometimes, this is just a result of the way the region of revolution is shaped with respect to the axis of revolution. In other cases, cavities arise when the region of revolution is defined as the region between the graphs of two functions. A third way this can happen is when an axis of revolution other than the x\text[/latex] or y\text[/latex] is selected. Since some surfaces are nonorientable, it is not possible to define a vector surface integral on all piecewise smooth surfaces.

This is in contrast to vector line integrals, which can be defined on any piecewise smooth curve. We have seen that a line integral is an integral over a path in a plane or in space. We can extend the concept of a line integral to a surface integral to allow us to perform this integration. The intersection of a plane that contains the normal with the surface will form a curve that is called a normal section, and the curvature of this curve is the normal curvature. For most points on most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures.

Any closed surface will have at least four points called umbilical points. At an umbilic all the sectional curvatures are equal; in particular the principal curvatures are equal. The sphere and plane are the only surfaces with this property. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry.

Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres. Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. The metric units of volume are cubic meters or cubic centimeters while the USCS units of volume are, cubic inches or cubic feet. The volume of sphere depends on the radius of the sphere, hence changing it changes the volume of the sphere.

There are two types of spheres, solid sphere, and hollow sphere. We will learn in the following sections about their volumes. About 1800 years prior to the discovery of calculus, Archimedes showed that the surface area of a sphere of radius is .

He also showed that the volume of a ball of radius is using the Cavalieri's principle, again without calculus . Archimedes invented a method that was later re-discovered and became known as Cavalieri's principle. This involves slicing solids with a family of parallel planes.

In particular, if we have two solids and if each plane cuts them both into cross-sections of equal area, then the two solids have equal volumes. It is far from obvious from the figure above how the cone and sphere add up to the cylinder. However, if we `rearrange' the conic volume, things become clearer. We note that a cone with half the height () has half the volume. So, we replace the cone by a double cone, each half of height , with centre-point at the centre of the sphere . Now it is clear that in a horizontal slice, the cross-section of the sphere is greatest at the equator and least at the poles.

Contrariwise, the cross-section of the cone is greatest near the top and bottom, and least near the centre-point. Thus, it is not unreasonable to speculate that the sum of the two cross-section areas might be equal. If a solid of revolution has a cavity in the center, the volume slices are washers.

With the method of washers, the area of the inner circle is subtracted from the area of the outer circle before integrating. Use the conversion formulas to write the equations of the sphere and cone in spherical coordinates. Also on that page you will see an explanation of the 4/3 in the volume of the sphere.

In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere. The volume of a pyramid is 1/3 times the area of the base times the height. Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle.

The sphere is there for comparison; the cylinder has had a cone drilled out from the top and the bottom, leaving solid material around it. We're going to slice both the cylinder and the sphere at a height h above the center. Consider a sphere of radius r and divide it into pyramids.

In this way, we see that the volume of the sphere is the same as the volume of all the pyramids of height, r and total base area equal to the surface area of the sphere as shown in the figure. How to perform a triple integral when your function and bounds are expressed in spherical coordinates. In the following problems, students will calculate the volume of a sphere using the formula derived in the lesson. Then, students will derive the formula for the volume of a hemisphere using a similar integration technique. Last, students will use their new formula to find the volume of a specific hemisphere. The following picture is the cross section of the inscribed sphere along the plane, which then becomes a circle of radius inscribed in a square of side .

Volume Of A Sphere Derivation Integral There are so many examples of spherical objects in our day-to-day life. Just remember or derive the formula and calculate the volume for applications. Calculating the flux integral directly would be difficult, if not impossible, using techniques we studied previously. At the very least, we would have to break the flux integral into six integrals, one for each face of the cube. But, because the divergence of this field is zero, the divergence theorem immediately shows that the flux integral is zero.

States that given two solids of the same height, whose cross-sections, taken at the same distance above the base, are of equal area, then the solids have the same volume. In this blog, I used polar coordinates to derive the well-known expression for the area of a circle, . In today's blog, I will go from 2 to 3-dimensions to derive the expression for the surface area of a sphere, which is . To do this, we need to use the 3-dimensional equivalent of polar coordinates, which are called spherical polar coordinates.

He rose to the challenge masterfully, becoming the first person to calculate and prove the formulas for the volume and the surface area of a sphere. The method he used is called the method of exhaustion, developed rigorously about a century earlier by one of Archimedes' heroes, Eudoxus of Cnidus. Ok, now let's get a sphere of radius R and slice it in half to make a hemisphere. Next we'll get a cylinder of radius R and height R, and we'll scoop a cone out of it to make a sort of bowl . The following video shows how to solve problems involving the formulas for the surface area and volume of spheres. For the following exercises, draw the region bounded by the curves.